
Utazzunk az időbe! A boldog időbe, amikor matematika órán ültünk és H tanár úr magyarázott.
A határérték, … a limes … egy függvény azon tulajdonsága, … hogy a függvény argumentuma … műveleti sora … egyre közelebb kerül valamilyen véges értékhez … vagy a végtelenhez … Tegyük fel – folytatta – hogy az f (x) függvény értelmezve van egy nyílt intervallumon, amelynek x0 eleme … kivéve esetleg magát az x0 helyet. De a többin igen … Ha az f (x) függvényértékek tetszőlegesen közel kerülhetnek az A számhoz, amennyiben az x értékek eléggé megközelítik x0-t, akkor azt mondjuk, hogy f (x) az A számhoz tart miközben x tart x0-hoz; ezt gyakran úgy fejezzük ki, hogy f(x) határértéke A az x0 pontban A. Lehet, hogy sohase lesz az, de afelé tart. Azt, hogy f (x) határértéke az x0 helyen A, így jelöljük: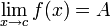
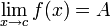
aztán még hozzátettet, ha bármely E > 0 számhoz van olyan B > 0 szám, hogy minden x esetén, ha 0 < |x − x0| < B, akkor |f (x) − A| < E. … Akkor f(x) tarthat A felé … Azok a limesek.
Ugorjunk jó tíz évet, amikor is egy tudásszociológiai szemináriumon találjuk magunkat, ahol azt mondják / kérdezik, hogy ugyanarról a szociális tényről eltérő ismeretek vannak ugyanabban a társadalomban – hogyan lehetséges ez? Aztán egy kellemetlen tapasztalat kerül említésre, nevezetesen hogy az emberek legyenek bármilyen okosak ugyanarról a tényállásról kialakított véleményüket képtelenek mások számára is evidenssé tenni. Beszélnek, közelítenek, szenzációsan közelítenek, de kifejezni nem tudják. Se megérteni a Másikat, se kifejezni magukat. Mert csak a limesek felé képesek mozogni. Csak „felé”. Nem oda, csak „felé”. Mindig csak "felé". A különbözőség megmarad. A kommunikáció jelentette sorozatban x sohasem lehet x0.







